Binary Search Tree



Binary search tree merupakan salah satu Teknik searching di dalam data structure. Binary search memiliki keunggulan jika dibandingkan dengan metode searching lainnya. Keunggulan Binary search adalah dapat men searching file dengan cepat, mensort dengan cepat dan dapat dengan mudah menginsert atau mendelete. Lalu apa bedanya binary search tree dengan binary tree? Binary search tree bisa dibilang merupakan versi sorted dari binary tree. Namun di dalam BST ada beberapa aturan yaitu:
-                 Subtree sebelah kiri selalu lebih kecil nilainya dari pada root node.
-                 Subtree sebelah kanan selalu lebih besar nilainya daripada root node.
-                 Subtree kiri dan kanan masing-masing juga harus berupa Binary Search Three.

Terdapat 3 buah operasi yang dapat dilakukan di Binary Search Tree
-                  find(x): Mencari node x di dalam sebuah BST.
-                  insert(x): memasukan node x baru kedalam BST.
-                  remove(x): Mendelete node x dari dalam sebuah BST.

Operasi find/search:
Seperti yang kita ketahui, salah satu keunggulan dari BST adalah bisa mencari data dengan cepat. Berikut adalah langkah operasi pencarian x dalam BST.
-        Operasi dimulai dari root sebuah BST. Jika x berada berada pada root maka pencarian sudah selesai.
-           Jika tidak terdapat di root maka dilanjutkan dengan melihat apakah x leibh kecil dari root      key atau lebih besar.
-           Bila x lebih kecil maka pencarian akan dilanjutkan ke subtree sebelah kiri secara rekursif.
-           Bila x lebih besar maka pencarian akan dilanjutkan ke subtree sebelah kanan secara            rekursif.

Operasi Insertion:

sumber: https://blogger.googleusercontent.com/img/proxy/AVvXsEg5m0k8s6IcTrBVZKFjARzWJRsZOs_1_LtT2hxDtION01HCeUqER6i7Ly27ebjKrYYkQ0JORXzenaUQ5IANUF9loQ8tAXpfuqEX6aUE_tjA_KYVA4H_CtpzB8T4_AeWMMQPBJ7ahrruimVeKqMluUBYrDQa5BbLl8iGESY47192E_lz=

Operasi ini memungkinkan anda dalam menginsert sebuah node ke dalam BST. Menginsert sebuah node ke dalam BST bisa dilakukan dengan mudah. Berikut adalah langkah dalam menginsert x.
-             Dimulai dari root sebuah BST. Lalu dibandingkan apakah x lebih kecil atau lebih besar         dari root.
-            Jika x lebih kecil dari root maka x akan diinsert di subtree sebelah kiri.
-            Jika x lebih besar dari root maka x akan diinsert di subtree sebelah kanan. 
Sumber: https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/

-        
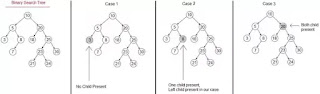
Operasi Deletion:
Sumber: https://qph.fs.quoracdn.net/main-qimg-fd652710dbeb9b064a6323aeff477005.webp

Di dalam BST, kita tidak hanya bisa melakukan insertion tapi juga deletion. Sama seperti pada Insertion, salah satu keunggulan BST yaitu penghapusan dapat dilakukan terhadap target node, bukan terhadap 1 subtree . Berikut adalah langkah dalam melakukan deletion x.
-           Jika x merupakan sebuah daun maka x bisa langsung di delete dari BST.
-           Jika x mempunyai satu child maka delete x dan hubungkan child dari x ke parent dari x.
-           Jika x mempunyai dua child maka node akan digantikan oleh node paling kiri dari Sub Tree Kanan      atau dapat juga digantikan oleh child paling kanan dari Sub Tree Kiri.

Referensi:
https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/
https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-
insertion/https://www.mahirkoding.com/struktur-data-binary-search-tree-bst/




Komentar

Posting Komentar

Postingan populer dari blog ini

AVL Tree

Gambar
Balanced Binary Search Tree Seperti yang sudah kita pelajari, tree merupakan suatu bagian dari struktur data yang memungkinkan melakukan operasi insert, delete , dan searching. Sayangnya, waktu yang dibutuhkan insertion, deletion, dan searching bergantung pada tingginya tree tersebut dimana makin besar height nya maka akan semakin lama. Hal ini yang menyebabkan mengapa menggunakan Binary Search Tree akan kurang efektif bila sedang mengerjakan sebuah data yang berjumlah besar atau banyak. Oleh karena itu, dengan menyeimbangkan height dari tree tersebut akan membantu mempercepat operasi insert, delete, dan searching pada sebuah tree. Tree dengan tujuan untuk meminimalkan height disebut dengan Balanced Binary Search. Contoh dari Balanced Binary tree adalah AVL tree dan Red Black Tree karena kedua tree tersebut sebisa mungkin akan meminimalkan height dari sebuah tree. AVL Tree AVL tree merupakan salah satu bagian dari self-balancing binary search tree. Bahkan AVL tree merupakan se...
Baca selengkapnya

Linked List

Gambar
Linked List Apa itu Linked list? Linked List adalah suatu struktur data yang terdiri dari urutan record data dimana setiap record data terdiri dari field dimana salah satunya menyimpan alamat dari record data selanjutnya. Seperti definisi di atas, Linked list merupakan bagian dari struktur data. Di dalam linked list terdapat sesuatu yang disebut node. Node merupakan elemen data yang telah terhubung atau dihubungkan dengan link. Terdapat 2 istilah yang sering kita dengar di dalam Linked list yaitu tail dan head . Di dalam linked list terdapat 2 hal yang bisa dilakukan yaitu insertion dan deletion. Dengan ini di dalam linked list dimungkinkan untuk menambah atau menghapus node baik dia tail head atau bukan keduanya. Linked list terdiri dari 2 tipe yaitu single linked list dan double linked list. Linked List VS Array Apasih perbedaan array dengan linked list? Seperti yang kita ketahui array relatif lebih mudah jika dibandingkan dengan linked list. Lalu kenapa kita harus menggunakan l...
Baca selengkapnya